
Задачи по 4 уроку
Задача.1.
Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня. Определить величину внутренних сил.
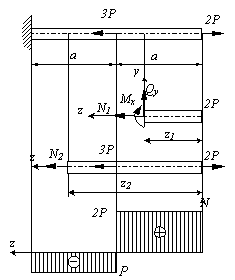


Решение.
Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Qy, Mx и уравновешиваяоставшуюся часть, получим:
Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.
Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось
Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Построим на первом участке линию параллельную оси z на высоте 2Р, на втором участке – линию со значением -Р. Области ограниченные графиком и осью z принято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.
Задача.2.
Построить эпюру продольных сил для жестко защемленной балки.

Решение:
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

3. По найденным значениям строим эпюру .
Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.

